Published as part of the ECB Economic Bulletin, Issue 3/2024.
This box looks at whether euro area inflation-linked swap (ILS) rates purely reflect inflation compensation – or if these also reflect “technical” factors, which would reduce their information content. When long-term ILS rates for the euro area peaked at 2.7% in summer 2023, their underlying drivers and their information content for monetary policy purposes came under scrutiny. Conceptually, ILS rates comprise the genuine inflation expectations of market participants plus inflation risk premia – referred to together as “inflation compensation” – in the absence of market imperfections. According to asset-pricing theory, risk-averse investors demand inflation risk premia as compensation for being exposed to inflation risk, which is typically positive in periods dominated by aggregate supply shocks.[1] However, owing to market imperfections, ILS rates may not solely reflect inflation compensation as narrowly defined above. For instance, a pension fund that was subject to regulation as regards its exposure to risks might be willing to pay more to hedge inflation risk than one would anticipate on the basis of its inflation expectations and a measure of uncertainty about the inflation outlook. Instrument‑specific liquidity risk premia could also create a wedge between ILS rates and pure inflation compensation. This box uses the catch-all term “technical factors” to cover all additional components arising from market imperfections.
We propose a simple econometric model which quantifies the share of total variation in euro area ILS rates that can be explained by inflation compensation in a narrow sense, thereby quantifying the role played by any technical factors. Our method adds a new econometric perspective and complements existing qualitative and quantitative approaches to identifying technical distortions in market-based measures of inflation compensation.[2] We do not decompose inflation compensation into genuine inflation expectations and inflation risk premia, instead regarding the two components as a single fundamental factor.[3]
Our econometric approach is based on the idea that all relevant information about pure inflation compensation (i.e. inflation compensation excluding any technical factors) should be reflected in nominal overnight index swap (OIS) rates. Conceptually, €STR OIS rates should comprise euro area real rates plus inflation compensation. Hence, we test the hypothesis that ILS rates mainly reflect inflation compensation by estimating the variation in ILS rates that can be explained by information inferred from OIS rates. We assume that nominal OIS rates are explained by a factor model: the OIS rate for each maturity is the weighted sum of a small set of (possibly unobservable) economic pricing factors, with each maturity having its own weights. Real OIS rates are assumed to be weighted sums of the same pricing factors, but with different weights. Accordingly, the (unobserved) inflation compensation contained in OIS rates is also, necessarily, a weighted sum of the underlying pricing factors. Suppose that observable ILS rates reflect not only fundamental inflation compensation, but also an ILS-specific technical factor (e.g. a liquidity premium). That additional driver would not form part of the aforementioned fundamental pricing factors. In that case, if we back out pricing factors from OIS rates (using statistical principal component analysis, for example) and regress ILS rates on those factors, any ILS-specific technical factors not covered by OIS rates will show up in the residual.[4],[5]
The share of total variation that is not explained by this simple econometric model constitutes an upper bound for the role of technical factors. If those technical factors are all absent, theory suggests that all variation should be explained by the fundamental factors, and the regression will thus achieve an of 1.[6] In practice, even in the absence of technical factors, such an extreme result seems unlikely for several reasons. First, the underlying OIS factors are not directly observable (requiring estimation on the basis of a finite sample). Second, there may be non-linearities in the relationship between OIS rates and the pricing factors (e.g. owing to the effective lower bound on nominal interest rates). Third, ILS rates are affected by an indexation lag, whereas OIS rates, being purely forward-looking, are not. And fourth, the pricing factors recovered from OIS rates may not capture “hidden” factors that have opposing impacts on the inflation compensation and real rate components of OIS rates such that those components offset each other completely.[7] By implication, this means that if the regression model, despite those reasons, still produces a high value for , technical factors are unlikely to be making a meaningful contribution to the dynamics of ILS rates.
Our empirical results suggest that euro area ILS rates mainly reflect pure inflation compensation, with little room for technical factors outside of some short-lived distortions in short-term ILS rates at times of extreme market volatility. Using the model outlined above, we regress ILS rates with maturities of one to ten years on the first three principal components inferred from OIS rates with maturities of between three months and ten years, as well as realised month‑on‑month and year-on-year headline inflation.[8] Overall, the regression model fits observed ILS rates very well, meaning that the fitted series closely reflect the observed levels and dynamics of ILS rates across maturities (see Charts A and B for one-year forward rates one year ahead and five-year forward rates five years ahead respectively).[9] This is also reflected in a high average of 0.9 across maturities (see the blue bars in Chart C), with the room for technical factors being slightly larger for the shortest maturities.[10] While the residuals are small on average, there are a few periods where they deviate more significantly from zero – most notably, the global financial crisis, the start of the COVID-19 pandemic and the aftermath of the Russian invasion of Ukraine. As those were periods of heightened market volatility, it is not unreasonable to think that the signal from market-based measures of inflation compensation could have been distorted somewhat by factors other than inflation expectations and inflation risk premia. However, the deviations are only short-lived, as reflected in the near-zero means for the residuals in each individual year in the sample, while the volatility of the residuals – as captured by their standard deviation – spikes in the years that include those episodes (see Charts A and B).
Chart A
Fit for one-year forward ILS rates one year ahead
(left-hand scale: percentages per annum; right-hand scale: percentage points)
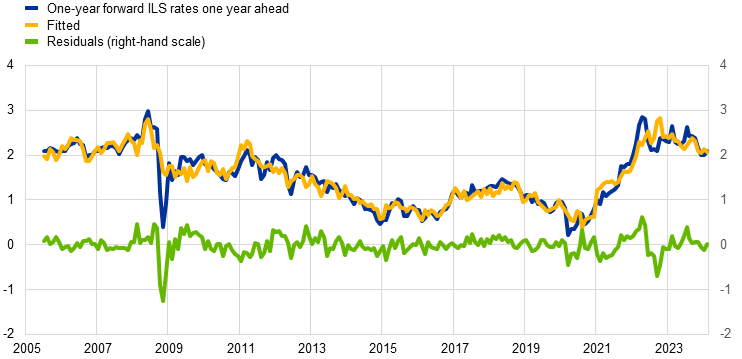
Sources: Bloomberg and ECB calculations.
Notes: This chart depicts: (i) one-year forward ILS rates one year ahead implied by observed spot ILS rates (blue line); (ii) fitted one‑year forward ILS rates one year ahead derived by regressing implied ILS forward rates on the first three principal components drawn from EONIA/€STR OIS rates and realised month-on-month and year-on-year HICP inflation in the euro area (yellow line); and (iii) the residuals for that regression, computed as the difference between observed and fitted ILS rates (green line). The latest observations relate to February 2024.
Chart B
Fit for five-year forward ILS rates five years ahead
(left-hand scale: percentages per annum; right-hand scale: percentage points)

Sources: Bloomberg and ECB calculations.
Notes: This chart depicts: (i) five-year forward ILS rates five years ahead implied by observed spot ILS rates (blue line); (ii) fitted five‑year forward ILS rates five years ahead derived by regressing implied ILS forward rates on the first three principal components drawn from EONIA/€STR OIS rates and realised month-on-month and year-on-year HICP inflation in the euro area (yellow line); and (iii) the residuals for that regression, computed as the difference between observed and fitted ILS rates (green line). The latest observations relate to February 2024.
Chart C
Variation in euro area ILS rates and break-even inflation rates that can be explained by OIS factors and realised inflation
(adjusted R²)
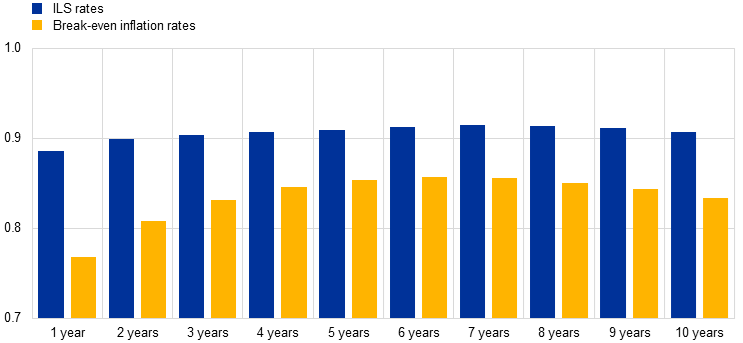
Sources: Bloomberg and ECB calculations.
Note: This chart depicts the R² derived by regressing euro area ILS rates and break-even inflation rates (BEIRs) on the first three principal components drawn from EONIA/€STR OIS rates and realised month-on-month and year-on-year HICP inflation in the euro area.
However, our analytical framework suggests that there is more room for technical factors in euro area BEIRs inferred from inflation-linked bonds. The regressions using BEIRs derived from the bond market generally have a lower (see the yellow bars in Chart C). This is consistent with the commonly held view that BEIRs are more prone to technical factors owing to the relatively low levels of liquidity in the ILB market.[11] These results suggest that the average of 0.9 achieved for euro area ILS rates is strikingly high and that such high levels of explanatory power are not common. In particular, such high levels are not seen in markets with relatively low levels of liquidity, such as the ILB market.
See Campbell, J.Y., Sunderam, A. and Viceira, L.M., “Inflation Bets or Deflation Hedges? The Changing Risks of Nominal Bonds”, Critical Finance Review, Vol. 6, No 2, 2017, pp. 263-301.
See Work stream on inflation expectations, “Inflation expectations and their role in Eurosystem forecasting”, Occasional Paper Series, No 264, ECB, 2021. The authors of that paper assess potential technical factors in ILS markets using analysis of market depth, activity indicators and regression analyses, estimating the sensitivity of ILS rates to bid-ask spreads for inflation-linked bonds (ILBs) and other liquidity indicators.
For more information on model-based decompositions of ILS rates into genuine expectations and inflation risk premia, see the box entitled “Decomposing market-based measures of inflation compensation into inflation expectations and risk premia”, Economic Bulletin, Issue 8, ECB, 2021.
In addition to the pricing factors inferred from OIS rates, our model also includes measures of realised inflation in order to account for the fact that, by contrast with OIS rates, ILS rates are subject to an indexation lag, which the OIS pricing factors may not properly reflect. The indexation lag means that the final pay-off for an ILS contract will depend on year-on-year inflation realised three months prior to the end of the contract.
It is possible that OIS rates are also driven by OIS-specific technical factors. This is not an issue, since such factors would simply be redundant for ILS rates: the ILS weights on such factors would be zero.
Speck, C., “Break-Even Inflation Rates for the Euro Area”, Discussion Papers, Deutsche Bundesbank, forthcoming, follows the same approach for bond-based break-even inflation. However, the analysis in that paper builds on principal components drawn from German Bund yields and does not – unlike this box – include other control variables such as measures of realised inflation.
In such a situation, OIS rates would not load on such factors, while inflation compensation would, and principal component analysis of OIS rates, for example, would not be able to identify those factors.
Realised inflation is included in order to account for the indexation lag in ILS rates. For example, a one‑year ILS contract in month t would be linked to inflation developments between t-3 and t+9, while a similar one-year OIS contract would be tied to €STR developments between t and t+12. In addition, we add a dummy that equals one as of 2021 and interaction terms with this dummy for all explanatory variables in order to account for the possibility that the recent period of high inflation might have caused a structural break.
Indeed, the results confirm that while a regression model based solely on OIS factors produces a good fit, adding realised inflation significantly improves that fit, particularly at shorter maturities where the indexation lag matters more. This is consistent with findings for the UK inflation market in Bahaj, S., Czech, R., Ding, S. and Reis, R., “The market for inflation risk”, Staff Working Papers, No 1028, Bank of England, 2023.
Although OIS and ILS rates are both persistent, with autocorrelations close to one, the level regressions do not appear to be spurious. Ex ante, if OIS and ILS rates were non-stationary, we would expect them to be cointegrated. Indeed, we reject the null hypothesis that the residuals are I(1) for all maturities, indicating that OIS and ILS rates are cointegrated (see Engle, R. and Granger, C., “Co‑integration and error correction: Representation, estimation, and testing”, Econometrica, Vol. 55, No 2, 1987, pp. 251-276).
The supply of bonds is constrained by the fairly mechanical issuance and tapping schedules of debt management offices, resulting in relatively low price elasticity of supply. It is a well-established fact that this relatively inelastic supply and the low total outstanding volume of €500 billion means that BEIRs based on government bonds contain a liquidity premium (see Fleckenstein, M., Longstaff, F.A. and Lustig, H., “The TIPS-treasury bond puzzle”, The Journal of Finance, Vol. 69, No 5, 2014, pp. 2151‑2197). In contrast, there are few constraints on the supply of ILSs, as any two market participants can essentially agree bilaterally to “create” a new swap at will, which is reflected in a very high price elasticity of supply.





