Investigating initial margin procyclicality and corrective tools using EMIR data
Initial margin (IM) reduces counterparty credit risk in derivative markets. Notwithstanding efforts to limit potential procyclical effects of IM-setting practices, there is an ongoing debate about whether the current framework sufficiently addresses this concern, in particular when Value-at-Risk (VaR) models are used for setting IM. This article provides further insights into this issue. First, using EMIR data, we provide an overview of outstanding IM in the euro area derivative market and identify the most relevant sectors for the exchange of IM. Second, using a VaR IM model in line with industry practice, we show that aggregate IM can potentially vary substantially over a long-term horizon. Finally, we show that an IM floor based on a standardised IM model could be an effective tool for reducing IM procyclicality.
1 Introduction
Initial margin (IM) and variation margin (VM) are important risk mitigants in derivative markets. IMs are exchanged between counterparties to cover against counterparty risk in derivative contracts in the event of default. VM is exchanged to reset the market value of the exposure arising from changes in prices of the underlying value to zero.
Concerns have been raised, however, about the potential procyclical effects of IM-setting practices on the wider financial market. In the aftermath of the global financial crisis, both academics[1] and policymakers[2] identified procyclical effects of IM-setting practices in derivative markets as a potential source of systemic risk. In times of economic buoyancy and low volatility, market participants tend to charge relatively low IMs and this allows derivative portfolios to grow, further compressing volatility and margins. IM tends to increase in times of crisis, thereby suddenly raising the funding requirements for derivative holders. The latter may alter their portfolio to adapt to the funding shock, which may subsequently trigger increased asset price volatility. This in turn feeds back into higher margins, setting in motion a vicious circle with potentially destabilising effects. As a result, IM-setting practices could have procyclical effects, increasing the magnitude of the swings in the margin, liquidity and leverage cycles.[3]
In the context of the work towards the G20 commitment of making derivative markets safer, policymakers have introduced new rules for IMs. The BCBS‑IOSCO framework was developed at the global level to govern the exchange of IMs in bilateral derivative trading and is currently being phased-in across several jurisdictions. Specifically, by specifying minimum requirements for IM models, this framework aims to ensure that the models are calibrated in a way so as to limit the procyclicality of the IMs they generate. Moreover, for transactions cleared by central counterparties (CCPs), CPMI and IOSCO have developed rules governing the risk mitigation techniques applied by CCPs, including rules for IM setting. In the European context, these frameworks have been implemented by means of the European Market Infrastructure Regulation (EMIR). Among other rules, EMIR requires that CCPs adopt certain “anti-procyclicality” (APC) tools to tackle procyclical effects of the margins they charge.[4]
Notwithstanding these efforts, there is an ongoing debate about whether the current framework sufficiently limits the procyclical effects of IM-setting practices. While some elements of the current regulatory framework (including the APC tools) were designed with a system-wide perspective in mind[5], the framework may not sufficiently take into account the system-wide externalities potentially arising from procyclical IM dynamics.[6] One particular issue is whether the calibration and application of the existing APC tools for cleared transactions, as well as the requirements for VaR IM models in the non-cleared space, are sufficiently robust to limit procyclicality.
Data available from EMIR reporting provides further insight into the relevance of IM-setting practices for the wider financial system. We contribute to this ongoing debate firstly by providing a detailed (and, to our knowledge, currently somewhat lacking) description of the initial margining landscape in euro area derivative markets. The EMIR database allows us to describe its key features, such as market structure and main actors.
Our analysis also adds to the discussion on the procyclicality of IMs and on the tools to address this issue. We use IM models in line with industry practice to assess the potential dynamics of IMs over a long cycle for a large set of outstanding interest rate derivatives. First, we use a historical Value-at-Risk (VaR) model to assess the procyclicality of IM computed with VaR-type models that are standard for cleared interest rate derivatives. Second, we employ the standard model for non-cleared derivatives, the Standardised Initial Margin Model (SIMM), to obtain an IM time series with relatively low procyclicality. This IM time series will serve as reference point for assessing the procyclicality of VaR-based IM. More importantly, in our analysis of the ability of policy tools to reduce procyclicality, the output from the SIMM model will be used to calibrate some of the tools.
Our findings suggest that an IM floor could be a simple and effective tool to reduce procyclicality, in particular by guarding against excessively low levels of IM. In our analysis, we discuss how policy tools could be more robustly designed to reduce procyclicality (intended in a statistical sense such as commoving with market volatility, for example), and hence help reducing potential procyclical effects, such as the amplification of the financial cycle, of IM-setting practices.[7] Among the tools considered, we judge an IM floor calibrated on the SIMM model[8] to be a promising tool for reducing procyclicality. Its novel design approach is relatively simple and relies on a standardised approach for calibration purposes, hence providing some safety against the optimisation of IM model output and against model risk. It may also be more effective than other tools in avoiding that IMs fall to levels considered excessively low from a macroprudential perspective.2
EMIR data on initial margins
Granular IM data made available through EMIR makes it possible to provide an overview of the exchange of IMs in euro area derivative markets. For our analysis we use the EMIR database maintained by the ECB, which includes transaction-level information on euro area derivative contracts for which at least one counterparty is based in the euro area. As required under EMIR[9], margins are calculated and reported on the basis of net positions resulting from a set of contracts (i.e. at the portfolio rather than the contract level).
The strong upward trend in IMs being exchanged in euro area derivative markets suggests that EMIR rules are having a significant impact. As can be observed in Chart 1, the total stock of exchanged IMs, as reported by euro area counterparties, increased from around €375 billion in the second quarter of 2018 to around €550 billion in the second quarter of 2019.[10] This trend is due to three factors in particular. First, the increasing share of centrally cleared derivatives, also driven by mandatory central clearing rules for new interest rate derivatives and credit derivatives. Second, the widening of the scope of counterparties subject to the exchange of two-sided IM exchange in non-centrally cleared transactions in line with the phase-in schedule of the BCBS‑IOSCO IM framework. Third, maturing legacy trades not yet subject to the obligation to exchange IMs are now being replaced by trades subject to IM exchange. The total stock of IM overestimates the amount of IM for which funding by market participants is needed. The IM posted by clearing members to CCPs for client portfolios is generally funded by IM posted by clients to clearing members. Controlling for this pass-through[11], we estimate that the amount of IM for which funding is needed from other sources is on average around 20‑30% lower (see orange line in Chart 1).
Chart 1
Total IM stock
(EUR billions)

Source: EMIR data available to the ECB.
Notes: IM stock is calculated by summing up paid and received IMs for all euro area counterparties. Double counting is avoided by only accounting for the paid IM in those cases where the receiving counterparty has also reported the IM. The effect of IM pass-through is approximated by subtracting 75% of the IM that is paid by clients to clearing members for cleared transactions from the amount of total IM.
Going forward, a further significant increase in the total IM across the euro area derivative market is to be expected. Currently, only around one-third of derivatives traded in terms of total notional value are fully collateralised, meaning that they are subject to the exchange of both the IM and the VM. Going forward, a further widening of the scope of bilateral margining requirements in September 2019 and September 2021, as well as the ongoing replacement of maturing trades not yet subject to two-sided IM exchange, will further increase the amount of the IM exchanged in euro area derivative markets.
At the sectoral level, banks and CCPs account for most of the IM paid and received in derivative markets. Figure 1 shows the amount of the IM exchanged among the different sectors, highlighting the central role of banks and CCPs[12]. The most significant IM flows take place from banks to CCPs, and within the banking sector. In line with the regulatory framework, CCPs are mostly receivers of IM but hardly pay any. All other sectors primarily pay the IM to counterparties in the banking sector and receive only a fraction of their paid IM back from these counterparties. Clearing members among banks subsequently pass on the received IM from their clients to their CCPs.
Figure 1
IM exchanged among sectors
(EUR billions)

Source: EMIR data available to the ECB.
Notes: Arrows indicate the IM paid from one sector to another. The size of the nodes represents total IM paid and received by the sector. Next to euro area counterparties, the data includes EU counterparties. Non-EU based counterparties are excluded due to the low data quality of their sector identifier. IF stands for investment funds, PF for pension funds, IC for insurance companies, OFI for other financial intermediaries. The reference date is 20 December 2018.
An entity level representation of the IM network sheds further light on the structure of the IM landscape. The three-tiered structure of the market, with the IM flowing from clients to clearing members and from these to CCPs, visible already to some extent in Figure 1, is more evident in Figure 2. Clients from all sectors exchange margins with the clearing members, which are primarily banks (the outer circle in Figure 2). These in turn typically perform the netting of their client portfolios and pay margins covering their net exposure to the CCPs (the inner circle in Figure 2). Some non-banks also make direct trades with CCPs and other non-banks, but these represent only marginal amounts of the IM exchanged in the system. The sizeable number of edges between entities other than CCPs indicates that the non-cleared market remains very large, also for trades between clearing members.
Figure 2
IM network at the entity level

Source: EMIR data available to the ECB.
Notes: Entity level representation of the IM exchange network. Nodes are scaled by the sum of the IM paid and received and are coloured by corresponding entity sector. Data includes all EU counterparties but excludes non-EU based counterparties due to the low quality of the sector identifier. Minor counterparties with amounts of IM paid and received of less than EUR 10mln are excluded. CCPs are located on the inner circle, clearing members are located on the outer circle. IF stands for investment funds, PF for pension funds, IC for insurance companies, OFI for other financial intermediaries, NFC for non-financial companies. The reference date is 20 December 2018.
In terms of derivative classes, it is estimated that most IMs are exchanged for equity and interest rate derivatives. To gauge the relative importance of different asset classes for the aggregate IM, we need to estimate the portion of total IM associated with a particular asset class. Since IM is only observed at the portfolio level, it is impossible to directly infer the total IM by asset class by aggregating from individual trades. However, based on the information on the composition of each portfolio, we can identify portfolios that are highly concentrated in a single derivative class and use the IM information for these portfolios to estimate the distribution of the IM across asset classes. Using portfolios with a concentration of above 80% in terms of the portfolio notional value[13], we estimate that equity derivatives contribute the most to the total amount of the IM exchanged, up to around 60%.[14] Interest rate derivatives contribute around 30%, the IM from foreign exchange and credit derivative markets together constitute about 5% of the total amount of the IM exchanged.
Overall, EMIR data suggest that IM-setting practices by banks and CCPs for equity and interest rate derivatives are important for aggregate IM dynamics. Our analysis highlights a concentration in banks and CCPs of the IM in the classes of equity and interest rate derivatives. This suggests that risk management practices governing the IM for these activities are particularly relevant for aggregate IM dynamics and may require further attention in any future regulatory work aimed at addressing potential systemic issues.
3 Simulation of the IM over the financial cycle
In this section we simulate the aggregate levels of IM for a subset of the interest rate derivative markets in the euro area over an entire financial cycle. The need for simulations arises from the fact that EMIR data on IM provides good coverage only starting from the end of 2017. Therefore, to obtain a better understanding of IM dynamics over a longer period (and in a “steady state”) and to contribute in a more meaningful manner to the debate on the procyclicality of the IM, we use simulation methods. The simulated margins will then be the base for investigating the impact of different policy tools aimed at reducing IM procyclicality, which we discuss in Section 4.
3.1 Portfolio selection and IM models
We select a large portfolio of interest rate swaps (IRSs) and compute the IM for this portfolio over a period of approximately nine years. To isolate the effect stemming from the IM models and abstract rebalancing effects from any one portfolio, we select a large portfolio consisting of around 87,000 outstanding EURIBOR-indexed IRS trades reported on 27 June 2018 in the EMIR dataset, representing 1,033 individual portfolios between 632 counterparties. The total portfolio has a notional value of €5 trillion, representing around 5% of the total euro area IRS market. We focus on IRSs because of their important role in financial markets, representing the largest class in terms of notional values.[15] For this set of trades, we compute the IM at the portfolio level taking into account netting effects for each counterparty pair over the period between mid‑2010 to end‑2018.[16][17]
The first model we use for the IM simulation is the Standardised Initial Margin Model (SIMM). This model was developed by the International Swaps and Derivatives Association (ISDA)[18] and provides a simple and standardised framework for calculating margins. It is the market standard in the non-cleared segment as is used by counterparties unwilling or unable to use more risk-sensitive but also more complex models, such as Value-at-Risk (VaR) models. For our simulation exercise, we use the calibration that was agreed by ISDA in 2018.[19] We generate a time series with the aggregate IM that SIMM would calculate for the entire portfolio of IRS derivatives through time. The time series will also be subsequently used in our analysis of policy tools as a benchmark for calibration purposes.
The second model we use is an exponentially-weighted historical Value-at-Risk model (EWMA VaR model). This EWMA VaR model is a variant of historical VaR-type models, widely used by CCPs and banks for computing IM, in particular in the cleared space and to some extent in the non-cleared space as well. In this model, the current volatility estimate depends on historically observed volatilities. This is then used to build VaR estimates of the derivative portfolio and the IM. We use this model because it reproduces faithfully the VaR-based model(s) used by CCPs in the EU.[20] Clearly, the time series produced by the VaR model is sensitive to the input parameters. We performed a number of sensitivity checks indicating that the qualitative nature of our results is supported. An extensive sensitivity analysis is however beyond the scope of this analysis given the computational intensity of computing the IM time series for a large portfolio.[21]3.2
Simulation results
Our findings suggest that the aggregate IM calculated according to the VaR model can vary substantially over time. The red line in Chart 2 shows that the VaR model can generate substantial swings in IM required for the IRS portfolio over time. For our calibration, we find that the aggregate IM may be as high as €3.1 billion and as low as €1.6 billion, with relative daily movements in the aggregate IM of up to 300 basis points. Clearly, the calibration of VaR models is an important quantitative factor, and as pointed out by Murphy et al. (2014) using a simple portfolio, the level of procyclicality of the IM computed by VaR models depends on the exact calibration. Hence, the IM time series obtained from VaR models should be considered as an example of what VaR models can produce, not as being fully representative of actual IM dynamics.
Chart 2
Simulation of the IM over a long-term horizon
(total IM in EUR billions)

Source: Author’s calculations based on EMIR data.
Notes: The red line represents the IM time series obtained from the VaR model. The corresponding y-axis is on the left. The blue line represents the IM time series obtained from the SIMM model. The corresponding y-axis is on the right.
The aggregate IM based on the SIMM model is less cyclical than the IM based on the VaR model. The amount of margin calculated according to the SIMM model (blue line) also varies but to a significantly lower degree, with relative daily movements in the total IM of only up to 20 basis points[22]. It was indeed designed to have low sensitivity to changes in market volatility and our analysis confirms previous findings that the SIMM is producing IMs with relatively low procyclicality.[23] This however comes at a cost. The more conservative design and calibration of the SIMM[24] lead to considerably higher IM levels, with the average IM for the VaR and the SIMM being €2.38 billion and €5.76 billion respectively[25]. This highlights the trade-off between volatility and level of IM required by the two models, with SIMM showing less volatility and less risk-sensitivity but higher levels of IM, compared to the VaR model.
4 Analysis of the impact of policy tools
Building on the two simulated IM time series, we analyse the ability of three policy tools to reduce VaR margin procyclicality. We consider the effectiveness of three tools in reducing the procyclicality of the IM computed with the VaR model. These tools fall broadly into the categories of tools that have been put forward in policy for in the past.[26] Compared to previous work, our selection of tools is primarily driven by the objective of considering those that are less open to discretion and minimise model risk. In particular, we present two tools with novel design features that rely for calibration purposes on the IM computed by the SIMM model, exploiting the lower procyclicality of the SIMM IM time series.
To assess the impact of tools on margin dynamics, we employ different measures of IM procyclicality and average IM levels. To be able to judge the effectiveness of the tools in reducing IM procyclicality, we present two measures of margin procyclicality and compute the reduction in these measures generated by the tools. We also assess the tools’ cost implications (i.e. the additional margin introduced by the tools) and their potential negative impact on the prudence of IM (i.e. the reduction in margin caused by the tools). In this way, we assess the performance of each tool along all its key dimensions: the reduction in procyclicality, the costs for derivative holders and the prudence of IMs.
4.1 Definition of tools and performance measures
The first tool we consider is a margin buffer built up during “good times” and released during periods of stress. We consider a buffer that is similar to the buffer APC tool in EMIR[27]. The buffer is defined as follows: in “good times” (i.e. when IM is relatively low), an additional amount of collateral is charged at the portfolio level between two counterparties in order to build a buffer that can subsequently be released once the margins increase[28], thereby reducing their disruptive rise (see left-hand panel of Chart 3 for an illustration). The buffer imposes higher margins in good times and then releases this additional collateral when margins reach stressed levels. Recognising the crucial role played by the calibration of the tool’s key parameters for the results, we evaluate the performance of the buffer under different calibrations. In particular, we vary the length of the build-up period of the buffer (i.e. the number of days before the buffer reaches its desired level) and assess the buffer’s impact on the key performance metrics for each build-up period length.
Chart 3
Illustration of policy tools
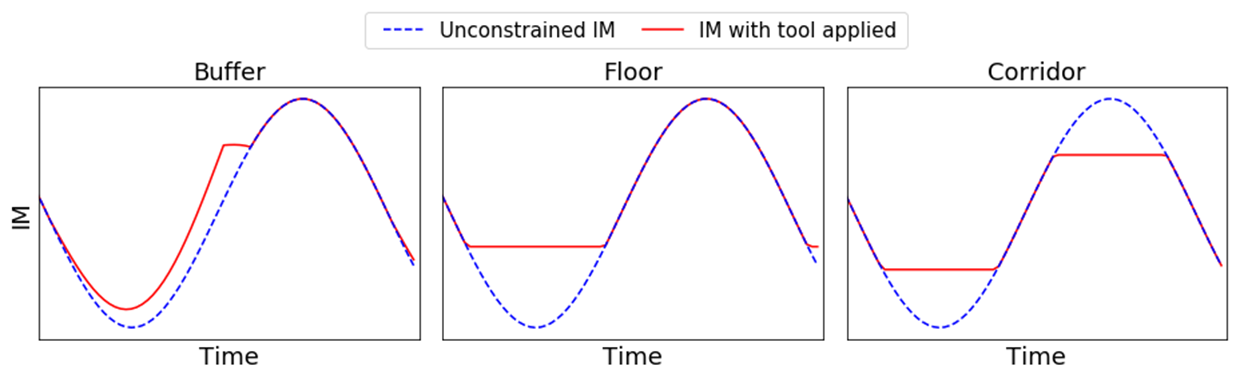
Source: Authors’ illustration.
Notes: The dashed blue line shows the evolution of the IM over time without the application of the policy tools. The red line represents the evolution of IM over time after one of the policy tools is applied.
We also consider a margin floor that is calibrated relative to the SIMM model. For a given portfolio, the floor to the VaR‑IM is defined as a percentage of the IM generated by the SIMM on the same day. Thus, under this tool the VaR‑IM can never fall below a certain fraction of the SIMM‑IM. As a result, the floor limits procyclicality by restricting how much the VaR‑IM is permitted to decline in good times. In order to assess the role of different calibrations for this tool, we vary the level of SIMM-generated IM at which the floor is set and assess the buffer’s impact on the key performance metrics for each floor setting.
Finally, we analyse a margin corridor that combines the floor with a ceiling. The ceiling, as part of the corridor tool, prevents the IM from being raised to high levels with the aim to limit the impact of abrupt IM calls. Like the floor, the ceiling is defined as a percentage of the SIMM. We vary the levels of SIMM‑IM at which the floor and the ceiling are set and assess the buffer’s impact on the key performance metrics for each setting. Tools like the corridor, which may prevent market participants from increasing margins, have been criticised in the past for their harmful effects on the ability of market participants to cover against counterparty risk. In our analysis, we therefore also aim to quantify the potential reduction in prudency caused by the tool. Our findings suggest that a corridor may indeed reduce prudency substantially, outweighing the benefits arising from the reduction in IM procyclicality achieved by such a tool.
We assess the performance of a tool by measuring the reduction in the procyclicality it achieves. We employ two measures of procyclicality that were proposed in related work[29]: i) a “peak-to-trough” measure representing the difference between the highest and lowest value of the margin simulated throughout the sample period; and ii) a “20‑day average increase” measure that provides the average of the top 10% increases of margins in 20 trading days. The first is a measure of long-term procyclicality in the sense that it measures the extremes that IMs can reach through the cycle. The second measure identifies short-term procyclicality, as it isolates the biggest increases that IMs experience in 20 trading days (i.e. approximately one month).
Besides the impact on procyclicality, we also assess how tools affect the costs and the insurance against counterparty risk associated with margins. By imposing restrictions on the IM generated by the VaR model, the tools may generate margins that lay above or below those that the VaR model would generate. In the first case we speak of “over-margining” (which increases the costs of holding derivatives positions) while in the second case we speak of “under-margining” (which decreases the ability of derivative holders to cover against counterparty risk). As a measure of “cost” of the tool we calculate the average increase in IM caused by each tool. Similarly, we compute the decrease in counterparty risk insurance (i.e. the “imprudence”) of the tool as the average decrease in margin caused by each tool.4.2
Results
The effectiveness of the tools in reducing procyclicality is measured as the reduction in the peak-to-trough and 20‑day average values triggered by the tools. The unrestricted VaR model shows a peak-to-trough of 1.91, implying that the highest margin paid through the cycle on our sample portfolio is 91% higher than the lowest margin paid on the same portfolio. The unrestricted VaR model also shows a 20‑day average increase of 0.16. Hence, in the months where the largest 20% jumps take place, the sample portfolio experiences a 16% increase in the IM.
The buffer has a mixed impact on the procyclicality measures. The left-hand panel in Figure 5 shows the procyclicality measures for the buffer, whereas the right-hand panel shows the cost-imprudence measures. The horizontal axis shows different speeds at which the buffer is built up.[30] For calibrations requiring a relatively quick build-up the buffer actually increases the peak-to-trough measure. This is intuitive if one considers that with a 1‑day build up period (at the very left of the graph), once triggered the buffer instantly adds 25% to the margin required, thus magnifying the jumps that the IM can experience. In contrast, we obtain a reduction in in the peak-to-trough measure as the period of the build-up is extended (i.e. as we move to the right on the horizontal axis of Chart 4). For example, for a build-up period of 150 days, the peak-to-trough measure is reduced by approximately 4%. We furthermore find that the buffer increases the average 20‑day-increase (see blue line in the right-hand panel of Chart 4) for all considered calibrations. This can be explained by the additional impact of the build-up of the buffer on increasing IMs over the considered 20‑day periods.
Costs associated with the buffer decline with the length of the build-up period. There is a negative relationship between the length of the build-up period and the costs associated with the buffer, with longer build-up phases associated with lower costs in terms of additional margins required. With a 150‑day build-up period, the buffer requires an additional 10.5% margin, on average (see yellow line in Chart 4)[31]
Chart 4
Margin buffer performance indicators
 Source: Author’s simulations.
Source: Author’s simulations.
Notes: The left-hand panel plots the reduction in procyclicality as measured by the peak-to-through (red line and left axis) and the average 20‑day increase (blue line and right axis) as function of the speed in the build-up of the buffer (horizontal axis). The right-hand panel plots the average increase in costs (yellow line and left axis) and imprudence (blue line and right axis) as function of the speed in the build-up of the buffer (horizontal axis).
The floor tool reduces procyclicality for all considered calibration values. Chart 5 shows the procyclicality measures (left-hand panel) for floor settings ranging from 0% to 50% of the SIMM model. We find that the floor can be very effective in reducing procyclicality. The peak-to-trough measure declines substantially as the floor becomes tighter (i.e. as we move to the right of the horizontal axis). The same is true for the 20‑day increase measure. For example, a floor equal to 20% of the SIMM reduces the peak-to-trough measure by 17% and the 20‑day increase measure by 22%.
Chart 5
Margin floor performance indicators
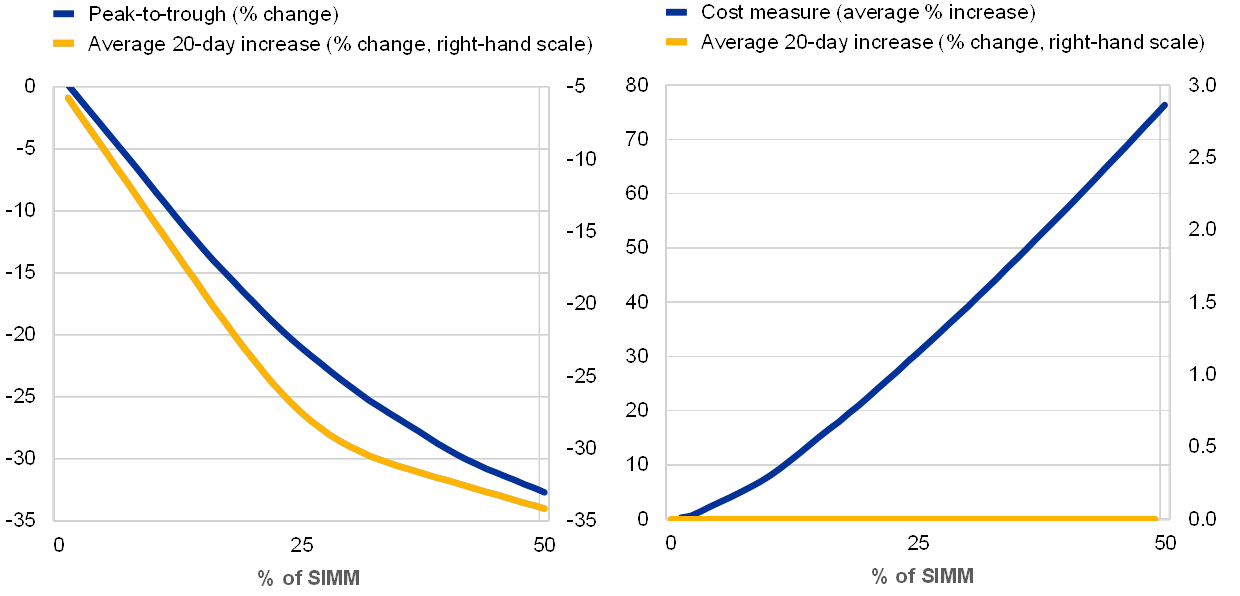
Source: Author’s simulations.
Notes: The left-hand panel plots the reduction in procyclicality as measured by the peak-to-through (red line and left axis) and the average 20‑day increase (blue line and right axis) as function of the % of SIMM‑IM at which the floor for the VaR‑IM model is set (horizontal axis). The right-hand panel plots the average increase in costs (yellow line and left axis) and in imprudence (blue line and right axis) as function of the % of SIMM‑IM at which the floor for the VaR‑IM is set (horizontal axis).
At the same time, the average IM increases with the tightness of the floor. The reduction in procyclicality comes at a cost: as shown by the yellow line in the right hand panel, the higher the floor is set as a percentage of the SIMM IM, the higher the costs for the derivative holder (i.e. the bigger the increase in the IM required on average). For example, setting the floor to 20% of the SIMM would increase the margin required by 23%, on average.[32]
Introducing a ceiling mirroring the floor can have strong positive effects on procyclicality but also a strong negative effect on the imprudence measure. As expected, adding a ceiling to the floor increases the procyclicality reduction achieved by the tool. For example, for a corridor value of 60 (i.e. for a floor of 20% and a ceiling of 80% of SIMM) the peak-to-trough measure and the 20‑day average increase measure are reduced by 25% and 37.5%, respectively (see Chart 6). As the corridor narrows (i.e. as the floor is set higher and the ceiling lower), both procyclicality measures decline substantially. Taking into account the cost measure, we find that the corridor is more effective in reducing procyclicality than the floor alone: it achieves lower procyclicality for the same cost. This, however, comes with reduced prudence: the imprudence measure shows how tighter ceilings cause substantial undermargining and thus weaken the insurance against counterparty risk guaranteed by IMs. Since the primary function of IM is to ensure against counterparty risk, limiting market participants’ ability to do so may come with serious negative side effects that should be taken into careful account when considering such tools.
Chart 6
Margin corridor performance indicators

Source: Author’s simulations.
Notes: The left-hand panel plots the reduction in procyclicality as measured by the peak-to-through (red line and left axis) and the average 20‑day increase (blue line and right axis) as function of the width of the corridor allowed, i.e. the difference between the % of SIMM‑IM at which the floor and the ceiling for the VaR‑IM are set (horizontal axis). A width of 100 implies that the floor is set at 0 and the ceiling at 100% of the SIMM‑IM. A value of zero implies that both the floor and the ceiling are set at 50% of the SIMM-IM. The right-hand panel plots the average levels of additional costs (yellow line and left axis) and of imprudence (blue line and right axis) as function of the corridor width (horizontal axis).
Overall, the results of our analysis indicate that the floor may be preferable to the other two tools. Among the tools considered, we judge the IM floor to be the most promising one for reducing procyclicality. Its novel design approach is relatively simple and relies on a standardised approach for calibration purposes, hence providing some safety against the optimisation of IM levels due to competition in financial markets. Compared to the corridor with its negative effect on prudency, a floor is superior since prudency is in our view a crucial consideration. Compared to the buffer, the floor relies on a much simpler design and calibration. Moreover, the effects of the buffer on procyclicality are found to be much more sensitive to the choice of the calibration parameters.
Our results also indicate the importance of carefully monitoring the calibration of tools. The analysis above shows that the effectiveness and benefits of the tools are sensitive to their calibration, highlighting the need to closely monitor the way in which any such tools are implemented in practice. In a similar vein, the ESMA guidelines on APC tools[33] emphasise the necessity to report on model specific parameters. In this regard, a key benefit of the floor considered in this article may be that its design is less open to discretion and minimises model risk.5
Conclusion
Our analysis sheds light on the Euro area IM landscape area and quantifies the relative importance of the different sectors and derivative classes. Our analysis of the current IM landscape confirms the crucial role played by banks and CCPs in aggregate IM dynamics. In terms of derivative classes, equity and interest rate derivatives account for the majority of the IM exchanged. These findings may be relevant for regulators and macroprudential policymakers when considering measures from a system-wide perspective.
We show that the IM computed with commonly used VaR models may exhibit significant volatility over time, in particular relative to the IM based on the SIMM model. Our simulation of the IM for the sample IRS portfolio shows that the IM based on VaR models can vary substantially over time. The magnitude of the variation in the IM required for this portfolio suggests that, in the aggregate, market participants may have significantly higher IM funding needs in some stages of the cycle compared to others, with potential system-wide implications.
Finally, our assessment of the impact of policy tools suggests that an IM floor based on the SIMM model can be a simple and effective tool to reduce procyclicality. Among the tools considered, we judge the IM floor as particularly promising. As its calibration is simple and relies on the SIMM model, it could be an effective tool in ensuring that IMs do not fall to excessively low levels, thereby reducing procyclicality. Moreover, the design of the floor based on a standardised approach may be considered superior to design approaches solely based on VaR-models. Our analysis also highlights that tools restricting market participants’ ability to increase margins should be considered very cautiously, given their impact on margins’ effectiveness as counterparty risk management tools. Finally, our analysis shows that the effectiveness and benefits of the tools are sensitive to their calibration, highlighting the need to closely monitor the way any such tool is implemented in practice.
6 References
Brunnermeier, M.K. and Pedersen, L.H. (2008), “Market Liquidity and Funding Liquidity”, The Review of Financial Studies, Vol. 22, No 6, pp. 2201‑2238.
Committee on the Global Financial System (2010), “The Role of Margin Requirements and Haircuts in Procyclicality”, CGFS Paper 36, Bank for International Settlements.
Constâncio, Vítor (2016), “Margins and haircuts as a macroprudential tool”, Speech, ESRB International Conference on the macroprudential use of margins and haircuts.
Battistini, N., Grill, M., Marmara, P. and van der Veer, K. (2016), “A Case for Macroprudential Margins and Haircuts”, Special Feature A, ECB Financial Stability Review, May 2016.
ESMA (2015), EMIR Review Report No 2: Review on the efficiency of margining requirements to limit procyclicality, ESMA, 13 August 2015.
ESMA (2019), “Guidelines On EMIR Anti-Procyclicality Margin Measures for Central Counterparties”.
ESRB (2017), “The macroprudential use of margins and haircuts”, Report.
Fontana, S., Holz auf der Heide, M., Scheicher, M. and Pellizon, L. (2019), “The anatomy of the euro area interest rate swap market”, ECB Working Paper, No 2242.
Glasserman, P. and Wu, Q. (2018), “Persistence and Procyclicality in Margin Requirements”, Management Science, Vol. 64, No 12, pp. 5705‑5724.
ISDA (2017), “ISDA SIMM 2.1 methodology”.
Jukonis, A. EPIC: an EMIR based derivative pricing and stress testing tool. (2019) Unpublished manuscript.
Krahnen, J. and Pelizzon, L. (2016), “Predatory Margins and the Regulation and Supervision of Central Counterparty Clearing Houses (CCPs)”, Safe Working Paper, 2016.
F.D. Lenoci, E. Letizia – Identifying counterparty sector in EMIR data – Box 1 in ECB Economic Bulletin Article 1 – Issue 6 (September 2019)
Maruyama, A. and Cerezetti, F. (2018), “Central counterparty anti-procyclicality tools: a closer assessment”, The Journal of Financial Market Infrastructure, Vol. 7, No 4, 2018.
Murphy, D., Vasios, M. and Vause, N. (2014), “An investigation into the procyclicality of risk-based initial margin models”, Bank of England Financial Stability Paper, No 29, May 2014.
Murphy, D., Vasios, M. and Vause, N. (2016), “A comparative analysis of tools to limit the procyclicality of initial margin requirements”, Bank of England Staff Working Paper, No 597, April 2016.
Bartholomew, H. (2016), “Equity derivatives now biggest consumer of initial margin”, Article, Risk.net, 2016.
Robertson, M. (2018), “Cleared and Uncleared Margin Comparison for Interest Rate Swaps”, CFTC Working Paper.
- See, for example, Brunnermeier and Pedersen (2009).
- See, for example, CGFS (2010) and ESRB (2017).
- Liquidity stress arising from variation margin (VM) calls has also been identified as a potential source of systemic risk but is not covered in this article. The focus of the VM-related issues is on liquidity needs following a shock in a financial market that alters substantially the market values of derivatives (see ESRB (2017)).
- In particular, CCPs should either: (i) ensure that margin requirements are not lower than those that would be calculated using volatility estimated from a 10‑year lookback period; (ii) assign at least 25% weight to stressed observations in a particular lookback period; or (iii) use a buffer that builds up during phases of relatively low margins to be subsequently released once margins reach a certain level. See Article 28 in Commission Delegated Regulation (EU) No 153/2013 of 19 December 2012.
- The BCBS‑IOSCO framework includes the reduction of systemic risk as one of its two stated objectives.
- See, for example, ESRB (2017), Battistini et al. (2016), Constâncio (2016) or Krahnen and Pelizzon (2016).
- It is important to note that the scope of our analysis does not allow for a complete assessment of whether IM setting practices have a causal impact on procyclicality in derivative markets and to what extent the considered tools ultimately reduce such potential effects. For the remainder of the article, the term procyclicality is used in the statistical sense, meaning a co-movement of the IM with market volatility and/or other cyclical variables.
- We impose that the IM of the VaR model cannot fall below a certain percentage of the IM generated by the SIMM.
- See Article 3 of Commission Delegated Regulation (EU) No 2017/148.
- Please note that EMIR data on IMs may also include collateral above the minimum IM requirements, a practice generally referred to as “overmargining”.
- The effect of IM pass-through is approximated by subtracting 75% of the IM that is paid by clients to clearing members for cleared transactions from the amount of total IM.
- Sectors of counterparties are identified using the classification of Lenoci and Letizia (2019).
- We do not observe the IM paid or received for each contract, but only for entire portfolios. However, we observe the breakdown of the portfolios by asset class. Hence, we can identify the portfolios that are concentrated in one asset type. We thus select those portfolios in which one asset class represents at least 80% of the portfolio’s notional value. With this criterion, we capture around 80% of the total amount of the IM in the euro area derivative market. The remaining 20% of the IM is associated with non-concentrated portfolios (i.e. portfolios in which no asset class represents more than 80% of the total notional value) and we assume that each class contributes equally to the IM for these portfolios.
- Bartholomew (2016) also suggests that equity derivatives have become the most relevant class for the IM.
- See, for example, Fontana et al. (2019) for an extensive discussion of the relevance of the IRS market. The analysis could be extended to other classes (in particular equity derivatives) in the future.
- Going back further in time is not possible due to the lack of available data needed as input for the model simulation.
- Market values are computed using the EMIR pricing tool described in Jukonis (2019).
- See ISDA (2017).
- ISDA plans to update some parameters on an ad hoc basis.
- For the calibration of the most important parameters of the model, we use a lookback period of five years, a margin-period-of-risk (MPOR) of five days and a relatively conservative decay factor of 0.99. We employ a weighting scheme which favours more extreme historical tail events when constructing the loss distributions. The weighting scheme is part of the EWMA model and rescales the shocks applied to the yield curve by the ratio of past and current volatility. Intuitively, if volatility of a risk factor today is much lower, the applied weight will be larger.
- See Murphy et al. (2014) for a detailed description of the EWMA VaR model and an in-depth sensitivity analysis for this model.
- We use different scales in the two vertical axes of Figure 4 for expositional purposes. In any case, measures of dispersion of IM changes show that the SIMM generates IM changes much more concentrated around their mean, compared with the VaR model.
- See Glasserman and Wu (2018) for a detailed discussion of the procyclicality of the SIMM IM.
- In particular the higher MPOR set by ISDA.
- This suggests that the SIMM produces higher margins for non-centrally cleared derivatives, and can therefore incentivise central clearing, in line with one of the key objectives of the overall regulatory framework. To note that Robertson (2018) shows that for some specific cases SIMM may also lead to lower margin requirements than VaR models.
- See, for example, ESRB (2017) for a discussion on a broader range of tools that could be used in this context.
- We consider the ability to release the buffer, as means of minimising the risk of other parameters in the VaR model changing in such a way as to offset the additional margin charged. The other two EMIR APC tools (10‑year lookback period and 25% stressed observations) result in margins that are arguably still solely a function of the VaR model (but with a longer lookback period and more weight on stressed periods, respectively). Notably, our VaR-model already incorporates a variant of the second tool as it employs a weighting scheme that puts more weight on stressed observations.
- In our exercise, we assume that the buffer is released once the IM charged by the VaR model moves above the 250‑day moving average.
- See, among others, Murphy et al. (2014) and Murphy et al. (2016).
- Starting from one day, equivalent to an immediate introduction of a 25% buffer, to 200 days, equivalent to a buffer reaching 25% after 200 trading days.
- Since the buffer can only increase the unrestricted VaR‑IM, it never causes undermargining and the imprudence measure equals zero for all calibrations.
- Since the floor only restricts margins from below, it never causes undermargining and the imprudence measure equals zero for all floor settings.
- See ESMA (2019). These guidelines are aimed at ensuring a common, uniform and consistent application of EMIR in order to limit procyclicality of CCP margins, including by providing guidance on the proper calibration and implementation of the APC tools.


