Coronavirus (COVID-19): market fear as implied by options prices
Published as part of the ECB Economic Bulletin, Issue 4/2020.
Introduction
Stock markets around the world have tumbled since late February, when international investors began to worry about the spread of the coronavirus outside of China and its impact on the global economy. Although equity markets have partially recovered since then, the Euro Stoxx 50 lost 12.3% in the week ending on 28 February, its largest weekly percentage loss since the global financial crisis in 2008. The S&P 500 declined by more than 11% in an equally catastrophic week. Overall, equity markets in the euro area and the United States lost around 35% of their value between their peak on 19 February and their trough on 23 March.
Chart A
Standard deviation of equity returns
(annualised percentages)

Sources: Authors’ calculations and Refinitiv.
Notes: Model-based estimates of the standard deviation of daily equity returns for four indices: the Euro Stoxx 50, the S&P 500, the FTSE 100 and the Nikkei 225. Daily data. The latest observations are for 13 April 2020.
The decline in equity prices has led to a large spike in the variance of their returns. The standard deviation of daily equity returns of major indices in the euro area, the United States, the United Kingdom and Japan is at levels comparable to the peaks associated with the October 1987 stock market crash and the default of Lehman Brothers in September 2008 (see Chart A). Recent turbulence has clearly been global in nature, as shown by the substantial jump in the standard deviation across indices. This is also reflected in a sharp rise, to values close to unity, in the bilateral correlations of equity returns for the four main equity indices, which highlights the presence of a common factor among these returns. The resulting lack of diversification opportunities also amplifies the potential losses faced by international investors.
The increased risk aversion that came on top of the heightened risks may have amplified the sell-off in equity markets and across a large range of assets more generally. Following the initial large sell-off in financial markets, an important question for policymakers when assessing the response to the crisis concerns the persistence of the impact of the restrictions related to the coronavirus on financial risk, financial conditions and, ultimately, on real economic activity. One of the main ways in which this shock has spread is via financial market linkages and, most notably, via the synchronous plunge in global stock markets. The sell-off may have been driven by an increase in the perceived amount of risk present in the markets, an increase in the reluctance of investors to take risks, or a combination of both. Knowing the main source of the decline in equity prices (and financial assets in general) may help policymakers understand its persistence and evaluate the policy response. The aim of this box is to assess the changes in the quantity and price of (tail) risks using an estimate of tail risk aversion based on the price of equity options.
Risk-neutral densities
The risk-neutral density of an equity price is the market’s estimate of the probability distribution for the future level of that equity price, adjusted for the presence of investors’ risk aversion. The risk-neutral density therefore reflects both the risk attitudes and price expectations of investors. Risk-neutral densities can be thought of as physical densities whose shape has been modified in order to give more prominence to those states of the world that are associated with particularly adverse outcomes and that, as such, result in lower marginal utility for investors.[1] We derive the risk-neutral density of future returns from the daily prices of call and put options traded on the Euro Stoxx 50.[2] On any given day, these options are available for more than one maturity, making it possible to estimate the risk-neutral density for the available range of maturities.
Fears of a market crash emerged in the early stages of the virus outbreak in Europe, but after the announcement of significant policy stimulus the expected upside potential for equity prices increased, even though market risks remained elevated. Chart B shows the Euro Stoxx 50 risk-neutral density for equity returns, backed out from options and spanning a horizon of up to one year, on three dates: (i) 21 February, just before the virus outbreak reached Europe in full force; (ii) a week later (28 February); and (iii) 20 March, after significant policy stimulus had been announced in the euro area and the United States. One can already observe a marked increase in the variance – as well as a fattening of the left tail – of the distribution in the week ending on 28 February, thus signalling increased fears of a market crash.[3] By 20 March, after significant monetary and fiscal policy measures had been announced and equity markets had already fallen sharply, the lower tail of the risk-neutral density remained broadly unchanged, but the distribution became more skewed to the upside, suggesting an increase in the expected recovery of equity returns.[4]
Chart B
Euro Stoxx 50 option-implied risk-neutral densities
For options with a horizon of approximately one year ahead
(densities)
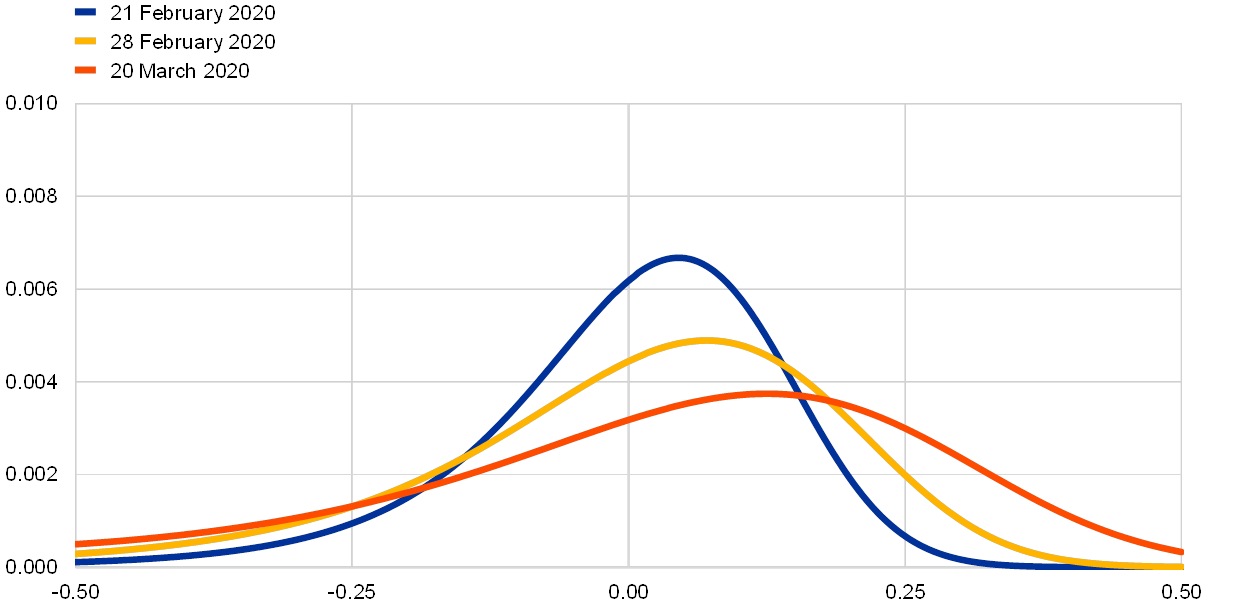
Sources: Authors’ calculations and Refinitiv.
Note: Risk-neutral densities of future returns backed out from the daily prices of call and put options traded on the Euro Stoxx 50.
A tail risk aversion indicator
An indicator of investor risk preferences or risk aversion can be derived by comparing the risk-neutral density with an estimate of the physical density of equity returns. The risk-neutral and the physical densities are related to each other through the pricing kernel, which embeds investors’ risk preferences. The physical density represents investors’ best judgement about probabilities of future price developments. Expectations of physical densities cannot be determined from market prices, as market prices also embed the risk preferences of investors. Researchers have turned to statistical methods to estimate such densities.[5] We use a daily multivariate generalised autoregressive conditional heteroscedasticity (GARCH) model to achieve this.[6]
The tail risk aversion indicator is constructed by comparing the left tails of the risk-neutral and physical distributions. Investors are risk-averse if they attach a higher risk-neutral probability to adverse events compared with the physical density. As tail risk-averse investors are willing to pay a premium to insure against the disutility associated with adverse outcomes, risk-neutral probabilities will overstate the corresponding physical probabilities for negative tail events. We look at the behaviour of the left tails of both the risk-neutral and the physical densities for equity returns over a three-month horizon. The index of aversion to negative tail risk of investors is calculated as the area to the left of the point on the risk-neutral density that corresponds to the lowest tenth percentile of the physical distribution of the returns (normalised by 0.1, i.e. the corresponding area on the physical density).[7] A tail risk aversion index above one indicates that investors fear the materialisation of negative tail events and are therefore willing to insure against such an occurrence by paying more than would be justified by its historical likelihood.[8] By contrast, an index value between zero and one could be considered as consistent with a situation in which appetite for risk is high.
Chart C
Euro Stoxx 50 tail risk aversion indicator and tail risk
For options with a horizon of 10 to 20 days ahead
(index)
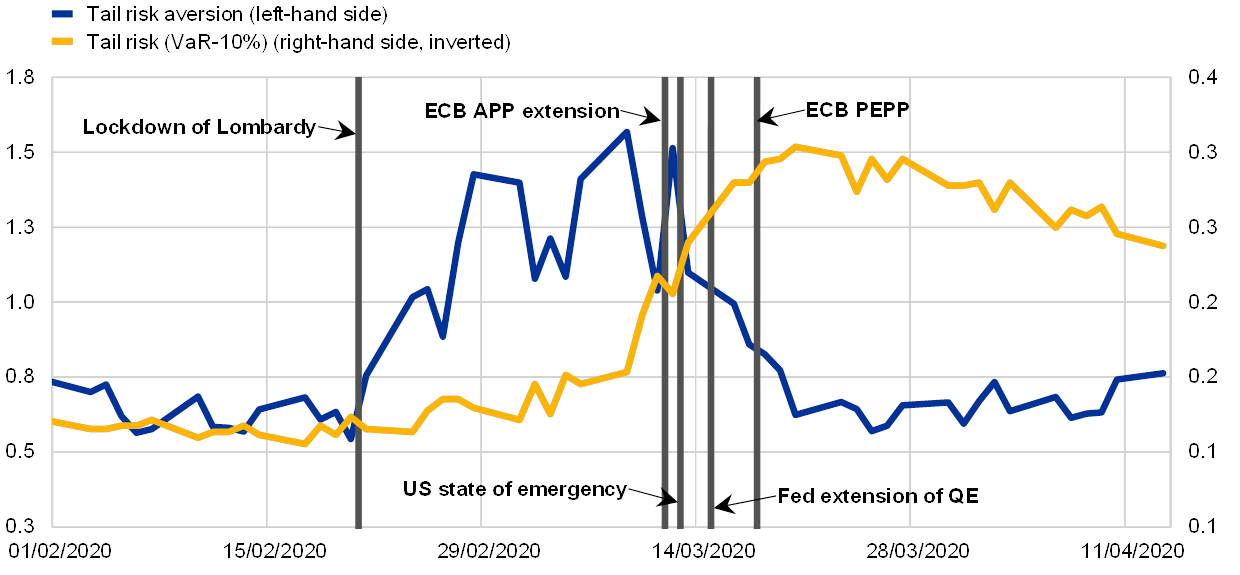
Sources: Authors’ calculations and Refinitiv.
Notes: “APP” stands for asset purchase programme and “APP extension” refers to the ECB measures announced on 12 March 2020, “PEPP” stands for the pandemic emergency purchase programme announced on 18 March 2020, “QE” stands for quantitative easing and “VaR” stands for value at risk (tenth percentile). The latest observations are for 13 April 2020.
The estimated tail risk aversion increased measurably from the second half of February. In mid-March, coinciding with the introduction of policy measures on both sides of the Atlantic, it reversed its course and returned to early-February levels. Chart C depicts the estimated tail risk indicator, along with a measure of tail risk, defined as the (inverted) tenth percentile of the physical distribution of the Euro Stoxx 50 returns. Initially, as the coronavirus was largely contained to certain regions in China, markets appear to have been rather complacent in the sense that there was practically no increase in tail risk aversion. At the outbreak of the pandemic in Europe, however, investors’ willingness to take on risk declined measurably, as reflected in the increase in the tail risk aversion index as of 21 February – the start of the lockdown in some parts of the Italian region of Lombardy. Around mid-March, the price of left tail risk started to decline again, as a cascade of fiscal and monetary policy measures was announced on both sides of the Atlantic. By contrast, tail risk itself remained broadly stable until the beginning of March, started to rise significantly thereafter and remained elevated even after the introduction of policy stimulus. One interpretation of these developments is that the measures put into place by central banks and governments have been able to support investors’ risk appetite, thus curbing the initial rise in the price of risk and leading it back to the value prevailing around mid-February. This reduction in the price of risk took place despite the rise in the amount of risk and therefore contributed significantly to minimising the impact of the shock on financial markets.
- Such modification results in investors being risk-neutral in the sense that all future cash flows from any asset can be discounted using risk-free rates.
- See Breeden, D. and Litzenberger, R., “Prices of State-contingent Claims Implicit in Option Prices”, The Journal of Business, Vol. 51, No 4, 1978, pp. 621-651, where the authors show that the second derivative of a call/put price function with respect to the strike price corresponds to the risk-neutral density function. For a detailed explanation of the method followed to perform the calculations, see Figlewski, S., “Estimating the Implied Risk-Neutral Density for the US Market Portfolio”, in Bollerslev, T., Russell, J. and Watson, M. (eds.), Volatility and Time Series Econometrics: Essays in Honor of Robert F. Engle, Oxford University Press, Oxford, United Kingdom, 2010.
- The large increase in variance, with investors pricing in a higher likelihood of both tails, overshadowed the increase in skewness.
- A similar picture emerges for equity returns backed out from options maturing at short horizons, i.e. with a residual life of 10 to 20 days.
- See, for example, Barone-Adesi, G., Engle, R.F. and Mancini, L., “A GARCH Option Pricing Model with Filtered Historical Simulation”, The Review of Financial Studies, Vol. 21, No 3, 2008, pp. 1223-1258.
- GARCH models account for the volatility clustering commonly observed in financial assets’ returns series, especially in periods of stress. At each date, we simulate a number of future paths of equity returns using this model, up to the maturity of the longest option traded that day in the market. From these returns, for a given maturity, we build their future physical density via kernel estimation. We estimate the expected physical density of equity returns by simulating their first and second moments using the full historical errors of the standardised residuals obtained by scaling the rates of change of an equity index with their conditional standard deviation based on the GARCH model. As this may overstate the variance of the errors in the presence of policy stimulus, an alternative would be to give more weight to errors recorded in the initial phase of the asset purchase programme in 2015 or to reduce the variance of the errors to mimic a decline in expected risks.
- The procedure is as follows: (i) determine the return associated with the lowest tenth percentile in the physical distribution, (ii) look up this return in the risk neutral distribution and calculate the area to its left, and (iii) divide this area by 0.1 (which represents the area to the left of the tenth percentile in the physical distribution).
- When the indicator is below one, investors are still willing to insure against the materialisation of negative tail events, but only at a lower price than that inferred from the historical likelihood. An indicator equal to one corresponds to a risk-neutral investor.


