Short-term forecasting of euro area economic activity at the ECB
Published as part of the ECB Economic Bulletin, Issue 2/2020.
1 Introduction
The real-time assessment of developments in economic activity is of central importance for the conduct of monetary policy. It facilitates the timely detection of changes in underlying economic dynamics in view of incoming data and contributes to a broader assessment of the economic outlook and associated risks. It is an integral part of the economic analysis in the European Central Bank’s (ECB) two-pillar approach to the assessment of the risks to price stability. Moreover, given the time lags in the transmission of monetary policy measures, a timely and reliable evaluation of economic conditions is a key element in the assessment of the monetary policy stance.
Official estimates of real GDP growth in the euro area are published with some delay, but current and near-term developments in real GDP can be assessed on the basis of high-frequency and timely indicators. Real GDP is the key variable summarising information on real economic activity. However, it is available only at a quarterly frequency and its first official estimate for the euro area, the preliminary flash estimate, is published only approximately 30 days after the end of the reference quarter. To fill this gap, econometric models have been developed at the ECB and elsewhere that can exploit a rich set of data to produce a real-time estimate of real GDP in the current and next quarter(s). Short-term forecasts typically rely on financial market data, business and consumer surveys or sectoral data (e.g. from industry, retail or external sectors). These predictors are often available at a monthly, weekly or daily frequency and with shorter publication delays.
There are a number of challenges to building quantitative tools for short-term forecasting of economic activity. First, these tools need to combine information from data collected at different frequencies. Second, they need to deal with the “ragged edge” of the data, which is due to the fact that different types of data are characterised by different publication delays. For example, industrial production in the euro area is published around six weeks after the end of the reference month, whereas opinion surveys and financial market data are often already available at the end of the reference period. Third, as there are many indicators that may be useful, the econometric approaches should be able to reliably estimate many parameters. Fourth, many indicators are subsequently revised and thus their first release might incorporate sizeable noise or measurement error. Fifth, data can be contaminated by outliers, caused by unusual events (e.g. strikes, atypical weather conditions), or changes in statistical properties over time, due to methodological or structural economic changes.
Further challenges for real-time forecasting became apparent in the course of the global financial crisis and in its aftermath. The vast majority of models, including those used at the ECB for short-term forecasting at the time[1], failed to predict the timing and depth of the Great Recession. In addition, these models systematically over-predicted the strength of the subsequent recovery. Several reasons were put forward at the time as an explanation for this disappointing forecast performance, including changes in structural relationships between economic variables, extreme outcomes in certain indicators that were inconsistent with model assumptions, insufficient coverage of financial market data and a non-linearity in the relationship between the real economy and the financial sector. Apart from addressing these shortcomings, recommendations for modellers included developing better tools for risk assessment and establishing appropriate economic narratives.[2]
The suite of models for short-term forecasting of euro area real GDP growth currently used at the ECB is the result of a comprehensive review conducted in 2015. The models rely on a medium-size data set of approximately 30 monthly indicators. A multivariate econometric set-up and a relatively broad coverage of various aspects of the euro area economy provide a framework for the interpretation of incoming data and forecast revisions. The forecasts are prepared using automated procedures (i.e. they are judgement-free) and can be produced in a matter of minutes. In addition to point forecasts, the model suite can also produce predictive distributions (fan charts). The latter can be used to assess, in real time, the degree of uncertainty around, or the risks to, the prevailing outlook for the short term.
The model-based short-term forecasts of real GDP are an important input to the Eurosystem/ECB staff macroeconomic projections.[3] By delivering quantitative estimates of real GDP growth ahead of the official data release and by providing an assessment of the macroeconomic “news” since the completion of the previous projection round, they are a useful starting point for updating the baseline short-term outlook for GDP growth. In addition, the predictive distributions provide model-based input for assessing the balance of risks surrounding the staff GDP projections.
The article is organised as follows. Section 2 explains the methodological framework of the suite of models for short-term forecasting of real GDP at the ECB. Section 3 presents an evaluation of the forecast performance of the models. Section 4 focuses on two interesting elements of the suite of models: news analysis and predictive distributions. Finally, Section 5 concludes with the main lessons learned and discusses the current challenges, further planned enhancements and new directions of work.
2 Methodological framework
Several types of models for short-term forecasting of real GDP have been proposed in the literature, including bridge equations, mixed-frequency dynamic factor models, mixed-frequency vector autoregressions and Mixed Data Sampling (MIDAS) models. Traditionally, “bridge equations”, linking GDP to a few key monthly indicators aggregated to a quarterly frequency, have been used. The latter are forecast using simple “auxiliary” models to complete the missing observations for the quarter. More recent approaches include mixed-frequency dynamic factor models and mixed-frequency vector autoregressions, which allow a single modelling framework to be used for the entire information set. Finally, MIDAS models allow data of different frequencies to be combined in a regression set-up by imposing a parsimonious lag structure. Different model types offer different advantages, in particular as regards robustness to structural breaks and extreme data outcomes or the possibility to interpret forecast revisions.[4]
The 2015 review of the ECB’s short-term forecasting models was motivated by the deterioration in the (relative) performance of the models in the course of the global financial crisis and in its aftermath. The suite of models used at the time encompassed (several versions) of bridge equations and large-scale mixed-frequency dynamic factor models. Both model types exhibited large forecast errors during the crisis and a positive bias (systematic over-prediction) thereafter, but the problems were more acute for the factor models. One of the reasons behind the positive bias was the insufficient coverage of the services sector and a declining contribution of the industry sector to value added in the euro area. Another reason was the difficulty to reliably estimate relationships between a large set of variables in view of their different behaviour during the financial crisis (in particular for survey vs. “hard”[5] data). The forecast performance of the mixed-frequency factor models appears to have been more sensitive to such structural changes compared with the performance of the bridge equations.
The current suite of short-term forecast models is based on bridge equations, in view of their comparatively better post-financial crisis forecast performance. Two types of bridge equations are included: (i) equations based on “hard” data, linking GDP to industrial production (excluding construction) and value added in services, and (ii) equations based on “soft” data, linking GDP to Purchasing Managers’ Index (PMI) composite output and PMI construction.[6] Both types embody the “supply” perspective for real GDP measurement[7], given that the coverage of information is more complete and timelier and the relationship with GDP is more stable compared with the “demand” perspective. As a consequence, the supply perspective results in more accurate forecasts. The forecasts for (quarterly) value added in services are obtained via an auxiliary bridge equation.
The monthly predictors included in the bridge equations are in turn forecast using “auxiliary” models and incorporate information from other monthly variables. Since bridge equations typically include just a few predictors, the only way to exploit a larger (and timelier) set of information in such a framework is through monthly auxiliary models to produce forecasts of the predictors.[8] The auxiliary models for the bridge equations are monthly Bayesian vector autoregressions and dynamic factor models. Both types of models allow a large number of variables to be incorporated.
The data set comprises approximately 30 indicators. It includes industrial production and business surveys for different sectors, monthly indicators of retail trade, unemployment, external trade and financial market data. The data set can be considered a “medium” size and is significantly smaller than those underlying the mixed-frequency factor models used previously. Forecast evaluations conducted during the review have shown that a very granular sectoral disaggregation typical for large data sets does not result in improved forecast accuracy.[9]
Forecasts are obtained as an average of forecasts produced by individual models. Combining two types of bridge equations with five auxiliary models results in ten distinct models for GDP. For point forecasts, an average of the individual model predictions is taken. Pooling individual forecasts leads to gains in forecast accuracy, even with respect to the best-performing model version[10], see below. Predictive distributions (densities) are produced via simulations and combined predictive density is calculated as an average of the individual model predictive densities. More technical details can be found in Box 1.
Box 1The suite of models for short-term forecasting of real GDP in the euro area: some technical details
The models used belong to the family of bridge equations. A bridge equation is a linear regression model where the dependent variable is the low-frequency variable of interest (e.g. quarterly GDP) and the regressors are higher-frequency predictors (e.g. monthly industrial production) aggregated to the lower frequency. In the case of the models for short-term forecasting of real GDP in the euro area described in the main text, the equations are specified as follows:
where
In order to obtain forecasts for GDP from the equations described above, it is necessary to obtain forecasts for the monthly predictors for the quarters of interest. For this purpose, “auxiliary” multivariate models at a monthly frequency are used: vector autoregressions (VARs) and dynamic factor models (DFMs).[12] The former are estimated with Bayesian methods, using a specification in first differences with six lags and the Minnesota prior with the degree of shrinkage dependent on the size of the model.[13] The latter are estimated by maximum likelihood, using the expectation maximisation algorithm.[14] The specification includes one single common factor, which follows an autoregressive process of order two and an autoregressive process of order one for the idiosyncratic components. Both types of models can deal with large sets of variables. VARs of three sizes (including two, 22 or 28 variables) and DFMs of two sizes (with 22 and 28 variables) are included. In order to handle the ragged edge caused by different publication delays of the variables, the models are cast into a state space representation and the Kalman filter and smoother are used to obtain the forecasts of the monthly variables and the weights for the news (see Section 4).
The variables for the bridge equations and the monthly “auxiliary” models were selected on the basis of several criteria including correlation analysis, in-sample and out-of-sample forecast performance, stability and significance of regression coefficients as well as shrinkage methods such as LASSO regressions.[15] The results confirmed previous findings in the literature that a very high level of disaggregation (100 series or more) is not needed to achieve the best forecast accuracy.
The computation of the models’ predictive distributions (densities) relies on the use of the Gibbs sampler and the simulation smoother (in order to handle the ragged edge).[16] The density forecasts from individual models are combined by a linear opinion pool with equal weights attached to individual densities. Combinations of normal densities produce distributions which can accommodate non-standard features such as fat tails or skewness. As for the case of point forecasts, pooling density forecasts is also an insurance policy against uncertainty in model selection.[17]
3 Forecast performance
A real-time evaluation is conducted of the forecasting accuracy of the models since their introduction and over a longer period starting in 2005. For this purpose, real-time data vintages going back to 2005 are constructed based on the information stored in the ECB’s Statistical Data Warehouse (SDW).[18] For each quarter in the evaluation sample, 12 forecast horizons are considered. The first forecast is obtained five months ahead of the first official publication. Subsequent forecasts are produced in semi-monthly intervals, up to two weeks before the publication of the preliminary flash estimate.[19] For instance, in the forecast cycle for the second quarter of the year, the first forecast would be produced at the end of January and the last one in the second week of July. The evaluation focuses on the bias and the root mean squared error of the forecasts. The forecasts are evaluated against the official flash estimates and the latest available vintage of quarter-on-quarter real GDP growth.
The forecast accuracy of the models is compared with that of the Eurosystem/ECB staff macroeconomic projections. For the purpose of the evaluation, a convention is adopted in line with which the latter are finalised in the middle of the second month of each quarter (corresponding to the forecast horizon of 1.5 and 4.5 months ahead for the current and the next quarter, respectively) and they remain unchanged in between.[20]
The accuracy of the models improves as new information arrives and the models fare relatively well compared with the Eurosystem/ECB staff macroeconomic projections. Chart 1 shows the root mean squared forecast error (RMSFE) and the bias for the model forecasts (light-coloured lines) as well as the projections (dark-coloured lines) compared with the official flash estimate (red lines) and with the latest vintage (blue lines) of GDP growth for the 12 forecast horizons considered. The evaluation period is 2015Q1 to 2019Q2.[21] Overall, the accuracy of the model forecasts is somewhat lower than that of the projections. The precision of the model forecasts gradually improves with a decreasing forecast horizon and the forecasts appear particularly useful at very short horizons after the projections have been finalised. Both the forecasts and the projections are more accurate and less biased when they are compared with the flash estimate than when they are compared with the latest available vintage of GDP.
Chart 1
Accuracy of model GDP forecasts and Eurosystem/ECB staff GDP projections over 2015Q1-2019Q2
(percentage points)
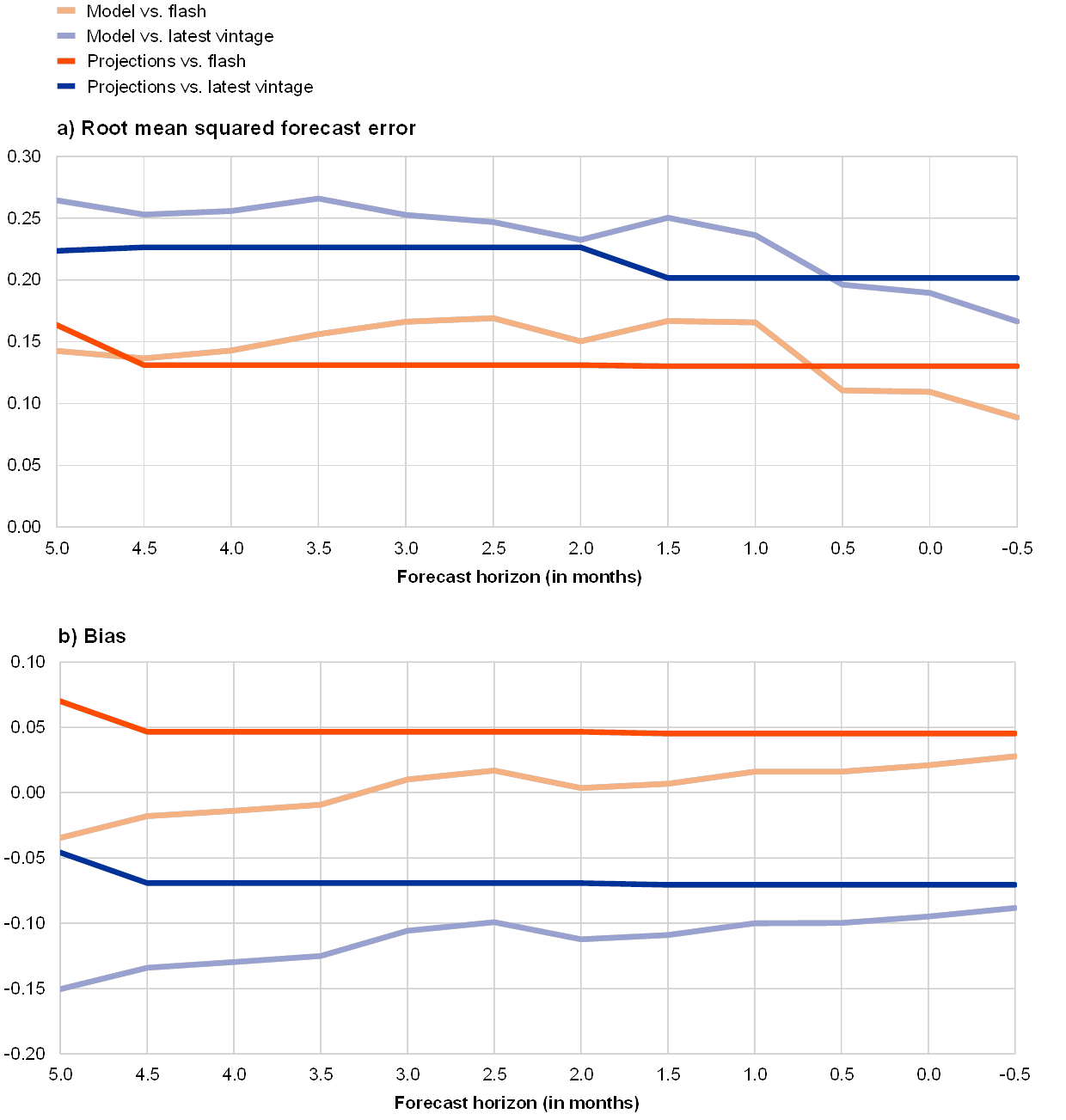
Source: ECB calculations.
Notes: For each quarter a sequence of 12 real-time forecast updates is evaluated. The forecast horizon (indicated on the horizontal axis) is defined as the distance (in months) between the end of the reference quarter and the date when the forecast was made. A convention is adopted in line with which Eurosystem/ECB staff macroeconomic projections are finalised around the middle of the second month of each quarter (1.5 or 4.5 months before the end of the reference quarter). Bias is defined as the average difference between the forecast and the outcome. Model forecasts and the projections are evaluated against the official flash estimate of GDP growth (released in the middle of the second month of the following quarter) as well as against the latest available vintage of real GDP growth.
The models also perform relatively well when evaluated over a longer period. The evaluation period considered above is relatively short and less volatile than, for example, the preceding period, which included the financial and sovereign debt crises. Focusing on the RMSFEs for 1.5-month ahead horizon with the flash estimate as the reference variable, Chart 2 presents the evolution of forecast accuracy since 2005 over an eight-quarter window. Several observations can be made. First, unsurprisingly, the financial crisis period was characterised by much larger forecast errors, both for models and for the Eurosystem/ECB staff macroeconomic projections. By contrast, the errors were not particularly large during the sovereign debt crisis. Second, the average model forecast is more accurate than the projections in some periods (notably during the financial crisis but not in the latest period).[22] Finally, an average of forecasts from several models typically does as well as the best model in each month (which changes over time) and is thus a good hedge against model uncertainty.
Chart 2
Evolution of forecast accuracy since 2005
(percentage points, RMSFE over an eight-quarter rolling window)

Source: ECB calculations.
Notes: The chart shows the RMSFEs over a rolling window of eight quarters. The forecasts are updated in the middle of the second month of the reference quarter (forecast horizon of 1.5 months), around the finalisation date of the Eurosystem/ECB staff macroeconomic projections. The reference variable is the official flash estimate of quarter-on-quarter real GDP growth. ‘Average’ refers to the rolling RMSFE of the average point forecasts (from ten different models). ‘Individual models’ indicates the range given by the minimum and maximum (rolling) RMSFE of the individual models. Shaded areas indicate recession periods (the Great Recession and the sovereign debt crisis) in the euro area as identified by the CEPR Business Cycle Dating Committee.
4 News analysis and a measure of risks
4.1 News analysis
The current framework allows linking revisions to the GDP growth forecast to model-based surprises or news content in releases of monthly predictors. This is also known as model-based news analysis and is an important element of data monitoring. The news (or surprise) for each indicator is defined as the difference between the released value of that indicator and its expected (forecast) value, i.e. the forecast error made by the model. The difference between two consecutive forecasts of GDP, that is the forecast revision, can be expressed as a weighted average of the news in the data released between the two forecast updates (plus the effect of historical data revisions and parameter re-estimation).[23] The weights reflect the average volatility of the news and its relevance for GDP. The sign of the news indicates whether the released number was better or worse than expected (“positive” or “negative” news).
Forecast revisions for individual quarters can be decomposed to identify the role of specific (groups of) indicators. Chart 3 illustrates this type of analysis taking the second quarter of 2019 as an example. The green line represents the evolution of the (average point) forecasts starting at the beginning of February up to mid-July, approximately two weeks before the release of the preliminary flash estimate of real GDP for that quarter. The bars indicate the model-based news or drivers of forecast revisions between the consecutive updates. A sizeable downgrade of the outlook at the end of March can be seen due to negative news in survey data. Subsequently, positive surprises on survey data lead to an upward revision of the outlook. From the end of May, the nowcast stabilises close to the outcome (preliminary flash estimate).
Chart 3
Model-based news and revisions to real GDP growth forecast for 2019Q2
(quarterly percentage changes and percentage point contributions)
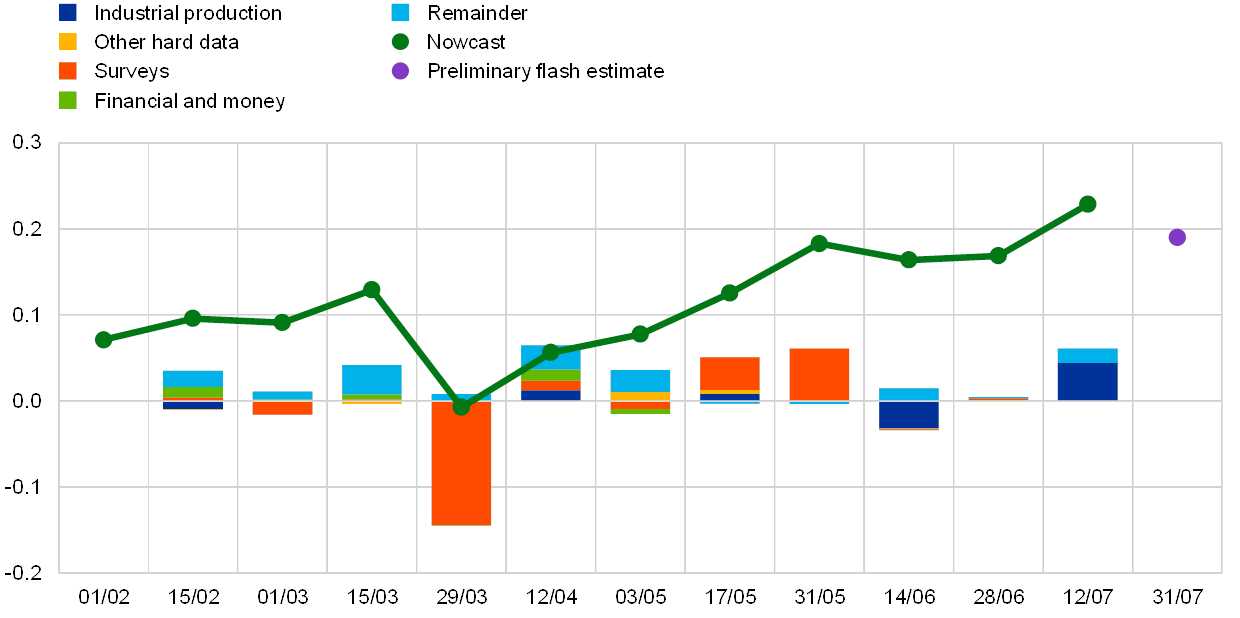
Source: ECB calculations.
Notes: The green line represents the average point forecasts (from ten different models) for real GDP growth in 2019Q2 from different forecast updates (indicated on the horizontal axis). The bars indicate the decomposition of forecast revisions between the consecutive updates into news stemming from different groups of data: ‘Industrial production’ – sectoral production indicators, ‘Other hard data’ – unemployment rate, external trade, retail trade, new car registrations, ‘Surveys’ – surveys of the European Commission and the Purchasing Managers’ surveys, ‘Financial and money’ – real money and financial and credit indicators. ‘Remainder’ collects the effects of data revisions and parameter re-estimation.
4.2 Density forecasts
The location and the shape of the models’ predictive distributions make it possible to assess the uncertainty around the point forecast as well as the direction and the degree of risks to forecasts from other sources such as the staff projections. For example, when the centre of the model predictive density (as represented by its mode or its median) is to the left of an alternative forecast, it signals downward risks to the latter and vice versa. Consequently, movements to the left or right of the predictive density will imply changes in the assessment of the direction of risks. By contrast, changes in the shape of the distribution (i.e. dispersion or concentration) will imply changes in the level of uncertainty. In real-time analysis, as more information is accrued over the forecast cycle, the predictive distribution usually becomes more concentrated, entailing less uncertainty surrounding the central forecast. It cannot be ruled out, however, that the release of one or several indicators could lead to a flatter distribution, due to diverging interpretations by the different models, and therefore to higher uncertainty.
As an example, predictive distributions indicate that, on the basis of these models, initially there were downward risks to the June 2019 Eurosystem staff GDP projection for 2019Q2 and the balance of risks became more neutral as more data became available. Chart 4 presents the models’ predictive densities for 2019Q2 obtained with the data available on 17 May 2019 (around the finalisation of the June 2019 staff projection) and on 12 July 2019. Initially, the models suggested downside risks to the projection since the probability of a lower outcome was higher than 50% (i.e. 60%). As more information became available by mid-July, the distribution moved to the right and became more concentrated. This means that the risks to the projection became more balanced (given that the probability of observing an outcome either above or below the projected value was around 50%) and smaller.
Chart 4
Predictive densities for real GDP growth in 2019Q2
(horizontal axis: quarterly percentage changes, vertical axis: density)

Source: ECB calculations.
Notes: The blue and yellow lines represent the (combined) predictive densities for real GDP growth from the respective forecast updates. The combination involves densities from the ten different models via a linear prediction pool with equal weights. The green line corresponds to the outlook in the June 2019 Eurosystem staff macroeconomic projections, and the red line is the preliminary flash estimate.
5 Conclusions and new directions
Changes in economic relationships caused by the evolving economic environment are a challenge to forecasting models in general and to short-term forecasting tools in particular. Some notable examples of structural changes include climate change, inter-sectoral re-balancing, developments in productivity, effects of severe recessions and, more specifically for the euro area, changes in the automotive industry.
Several lessons on how to address those and other challenges can be drawn from the experience with model-based short-term forecasting of real economic activity at the ECB. First, it is important to have several models in the toolbox and to assess their performance regularly, as it may deteriorate over time. Second, a combination of forecasts from different models typically helps to make the forecast performance more robust to misspecification. Third, including information on all major sectors of the economy is important but it is not necessary to use data sets at a very high level of disaggregation. A medium-size set of relevant and timely indicators appears to be sufficient to capture the information on real activity developments in the near term. Finally, it is important to be able to interpret the revisions to the outlook and to communicate uncertainty surrounding the forecasts. Still, scope for further improvement along several dimensions remains.
One issue is the high reliance of short-term forecasting models on survey data. Surveys provide qualitative information (i.e. opinions or perceptions) from relatively small samples of firms or consumers. They are very relevant due to their short publication lag. However, their relationship with quantitative (hard) indicators can change over time, reflecting either sampling biases (e.g. survival bias, especially after the crisis) or the fact that survey respondents can change the benchmarks used for their assessments (e.g. value of sales growth which can be considered an improvement in the firm’s performance).[24] As a result, the mapping of survey data levels into economic growth rates is not straightforward. For instance, at the beginning of 2018 survey data were at historically high levels[25], while real GDP growth slowed down considerably in the euro area. Conversely, some of the surveys painted a rather bleak outlook for 2019, while hard data turned out somewhat more resilient.
Alternative models and indicators can be employed to further enhance the accuracy and robustness of the models currently employed. Examples include time-varying parameter models that can deal with relationships that change over time in a flexible way.[26] The usefulness of alternative indicators and methods is also being investigated, in particular of machine learning algorithms and “big data”. The term “big data” is rather broad. In this context, it includes large and near-real-time data from the internet (e.g. internet search volumes[27], data from social networks such as Twitter and Facebook, newspaper articles) or large-volume data from non-official sources (e.g. from trading platforms and payment systems). Big data allows a wider range of indicators to be used, which can provide new and unique insights helpful for forecasting. For instance, text-based sentiment indicators could be particularly useful given that they can be produced automatically at a high frequency and at lower costs than survey-based sentiment indicators, and they can be based on large samples of newspapers to avoid biases.[28] At the same time, one has to keep in mind that considering a large set of explanatory variables entails risks of overfitting, not necessarily leading to improvements in out-of-sample forecast accuracy. Some of these challenges can be addressed by machine learning algorithms, which also have the advantage of potentially capturing complex non-linear relationships. These are some interesting directions for future work.
- See “Short-term forecasts of economic activity in the euro area”, Monthly Bulletin, ECB, April 2008.
- See, for example, Kenny, G. and Morgan, J., “Some lessons from the financial crisis for the economic analysis”, Occasional Paper Series, No 130, ECB, 2011.
- See “A guide to the Eurosystem/ECB staff macroeconomic projection exercises”, ECB, July 2016.
- See Bańbura, M., Giannone, D., Modugno, M. and Reichlin, L., “Now-casting and the real-time data flow”, in Elliott, G. and Timmermann, A. (ed.), Handbook of Economic Forecasting, Vol. 2A, North Holland, 2013, pp. 195–236, for a detailed review and list of references for the different modelling approaches.
- “Soft” is typically used to label indicators that reflect market expectations, most notably surveys and financial market data. By contrast, “hard” indicators often measure certain GDP components directly (e.g. industrial production).
- See de Bondt, G.J., “A PMI-based Real GDP Tracker for the Euro Area”, Journal of Business Cycle Research, Vol. 15, Issue 2, 2019, pp. 147–170.
- See Hahn, E. and Skudelny, F., “Early estimates of euro area real GDP growth – a bottom-up approach from the production side”, Working Paper Series, No 975, ECB, December 2008.
- See Bulligan, G., Golinelli, R. and Parigi, G., “Forecasting monthly industrial production in real-time: from single equations to factor-based models”, Empirical Economics, Vol. 39, Issue 2, 2010, pp. 303-336.
- This is in line with the conclusions in, for example, Bańbura, M., Giannone, D. and Reichlin, L., “Large Bayesian vector autoregressions”, Journal of Applied Econometrics, Vol. 25, Issue 1, 2010, pp. 71–92, and Bańbura, M., Giannone, D. and Reichlin, L., “Nowcasting”, in Clements, M.P. and Hendry, D.F. (ed.), The Oxford Handbook of Economic Forecasting, 2011.
- See Kuzin, V., Marcellino, M. and Schumacher, C., “Pooling versus model selection for nowcasting GDP with many predictors: empirical evidence for six industrialized countries”, Journal of Applied Econometrics, Vol. 28, Issue 3, 2013, pp. 392-411.
- See, for example, de Bondt, G.J., op. cit., for more details on the second equation. Note that the two equations result in better forecast accuracy than an average of (a large number of) single variable bridge equations.
- This results in higher forecast accuracy compared with using a univariate ARIMA model for each monthly predictor, in line with the findings in Rünstler, G. and Sédillot, F., “Short-term estimates of euro area real GDP by means of monthly data”, Working Paper Series, No 276, ECB, September 2003.
- See Bańbura et al., “Large Bayesian vector autoregressions”, op. cit.
- See Bańbura, M. and Modugno, M., “Maximum likelihood estimation of dynamic factor models on datasets with arbitrary pattern of missing data”, Journal of Applied Econometrics, Vol. 29, Issue 1, 2014, pp. 133–160.
- Note that the selection of indicators was not conducted in real time but in sample. However, as the data set was frozen at the beginning of 2015, the evaluation starting in 2015 is truly real-time. LASSO and similar techniques have been used to select variables for bridge equations in, for example, Bulligan, G., Marcellino, M. and Venditti, F., “Forecasting economic activity with targeted predictors”, International Journal of Forecasting, Vol. 31, Issue 1, 2015, pp. 188-206.
- See Durbin, J. and Koopman, S.J., “A simple and efficient simulation smoother for state space time series analysis”, Biometrika, Vol. 89, Issue 3, 2002, pp. 603–615.
- Geweke and Amisano showed that pooled forecast densities produce superior predictions, even if the set of models to be combined exclude the “true” model. See Geweke, J. and Amisano, G., “Optimal prediction pools”, Journal of Econometrics, Vol. 164, Issue 1, 2011, pp. 130-141.
- For a given date stamp and indicator identifier, a time series available at that date can be recovered from the SDW. Thus real-time data vintages reflect both publication delays and data revisions (as opposed to pseudo real-time vintages that reflect only the former).
- This reflects the frequency and the forecast horizon of the regular updates of short-term forecasts at the ECB. They are generally conducted twice per month, following the release of industrial production in the middle of each month, and of opinion surveys at the end of each month. The forecasts are always reported for the next two quarters to be published.
- As a consequence, the accuracy of the projections reported in Chart 1 changes in the middle of the second month of each quarter as a new projection becomes available. The projections are customarily finalised between the middle and the end of the second month of each quarter.
- Since no changes have been implemented to the models since 2015, this is a truly real-time out-of-sample evaluation.
- It should be noted that although the estimation of and the forecasts from the models are performed using real-time data, the specification and the choice of the variables in the new models were performed after the crisis and therefore have the benefit of hindsight for the evaluation period prior to 2015.
- See Bańbura et al., “Now-casting and the real-time data flow”, op. cit. For a meaningful analysis, the news should be based on multivariate models, incorporating most relevant indicators and taking into account differences in their timeliness and strength of the signal. The news analysed here is model-based and conceptually similar but not the same as “market surprises” (which are the differences with respect to market expectations).
- See Gayer C. and Marc B., “A ’New Modesty’? Level Shifts in Survey Data and the Decreasing Trend of ’Normal’ Growth”, European Economy Discussion Paper, 083, European Commission, July 2018.
- See the box entitled “The recent strength of survey-based indicators: what does it tell us about the depth and breadth of real GDP growth?”, Economic Bulletin, Issue 8, ECB, 2017.
- See, for example, Antolín-Díaz, J., Drechsel, T. and Petrella, I., “Tracking the Slowdown in Long-Run GDP Growth”, The Review of Economics and Statistics, Vol. 99, Issue 2, 2017, pp. 343–356.
- See, for example, Ferrara, L. and Simoni, A., “When are Google data useful to nowcast GDP? An approach via pre-selection and shrinkage”, Working Papers, No 2019-04, Center for Research in Economics and Statistics, 2019.
- See, for example, Thorsrud, L.A., “Words are the New Numbers: A Newsy Coincident Index of the Business Cycle”, Journal of Business & Economic Statistics, 2018.


